Placement de pôle par la méthode de Kessler

La fonction de transfert en boucle ouverte est de la forme:

$Fo_{(s)}=\frac{K_{ii}\tilde{K}(s+\frac{1}{T_{ii}})}{s(1+T_is)(1+T_Ms)}$

avec $\tilde{K}=\frac{K_t}{K_d}$. La fonction de transfert en boucle fermée est alors:

$F_{(s)}=\frac{K_{ii}\tilde{K}(s+\frac{1}{T_{ii}})}{s(1+T_is)(1+T_Ms)+K_{ii}\tilde{K}(s+\frac{1}{T_{ii}})}$

Si l'on considère que $T_M\gg T_i$ alors on se ramène à une fonction de transfert de la même forme que celle définie dans le placement de pôles par la méthode de l'optimum symétrique décrite au chapitre 5.1.4 à savoir:

$Fo_{(s)}=\frac{K_{ii}\tilde{K}(s+\frac{1}{T_{ii}})}{s(1+T_is)T_Ms}$

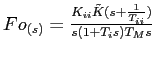
La méthode de KESSLER propose que l'on ait $a=4$ ce qui implique que $T_{ii}=4T_i$. Si $T_{ii}=T_M$ et que l'on néglige la constante de temps électrique $T_i$ devant la constante de temps mécanique alors la réponse est approximée comme étant celle présentée précédemment d'où l'on tire:

$K_{ii}=\frac{3K_dT_{ii}}{T_rK_t}$

De même, on a $K_{ii}=\frac{K_dT_M}{2K_tT_i}=\frac{J}{2K_tT_i}$. Afin de limiter la consommation de courant, on a vu que l'on applique une saturation sur la commande de $i_q$. Cela entraine alors un temps minimal $t_{min}$ pour atteindre la référence de vitesse désirée. En effet, si l'on reprend l'équation mécanique et que l'on considère que l'on régule le courant $i_d=0$ alors on a:

$t_{min}=\frac{-J}{K_d}\ln{\left(1-\frac{\Omega K_d}{i_{qmax}K_t-T_c}\right)}$ et si l'on néglige le frottement $K_d$ alors cette relation se simplifie en: $t_{min}=\frac{J\Omega}{i_{qmax}K_t-T_c}$

C'est avec ce temps minimal que l'on va définir le temps de réponse. Ainsi, dans notre exemple avec $i_{qmax}=55 A$, $\Omega=200 rad/s$ et à vide, on a $t_min\simeq0.54$ d'où: $K_{ii}=\frac{3K_dT_{ii}}{T_{min}K_t}\simeq 0.8184$ et $T_{ii}=T_M$. La réponse est donnée sur la figure 5.21.

Figure 5.21: Réponse en vitesse à vide.

Lorsque l'on applique un couple résistant $T_c=10 Nm$ alors on obtient la réponse de la figure 5.22.

Figure 5.22: Réponse en vitesse en charge $T_c=10 Nm$.

Une erreur apparait sur la réponse en régime permanent qui est dûe à cette charge. Cette réponse en vitesse est donc très dépendante de la charge de la machine et de la valeur de la référence de la vitesse. Si la réponse indicielle de la vitesse correspond à la constante de temps prédéfinie quand la machine est à vide, il n'en est plus de même quand un couple de charge est appliqué sur l'arbre. On obtient alors des fonctionnements très peu satisfaisants. Une autre approche, décrite dans [30], permettant le découplage du système comme vu au chapitre de la commande vectorielle, est envisagée et s'effectue alors par retour d'état non linéaire.