suivant: Régulateur intégral-avance de phase monter: Régulateur de courant précédent: Régulateur proportionnel Table des matières
En boucle fermée, on obtient alors:
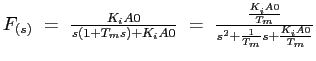
La pulsation propre du système (![]() ) vaut alors
) vaut alors
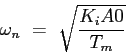 |
(5.5) |
et le coefficient d'amortissement ![]() est
est
| (5.6) |
Les conditions nous donnent alors:
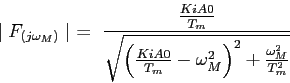 |
(5.7) |
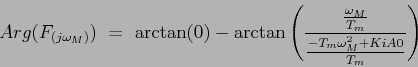 |
(5.8) |
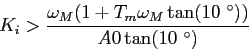 |
(5.9) |
 |
(5.10) |
Il existe donc une solution pour
![]() . Nous donnons la réponse de notre système pour
. Nous donnons la réponse de notre système pour ![]() lors d'un régime transitoire (cf.figure 5.4.a) et permanent (cf.figure 5.4.b).
lors d'un régime transitoire (cf.figure 5.4.a) et permanent (cf.figure 5.4.b).
On constate, en régime permanent, une ondulation sur la réponse dûe à la fréquence propre (![]() ) du système en boucle fermée définie par la relation 5.1.2 et qui vaut, pour notre exemple et pour
) du système en boucle fermée définie par la relation 5.1.2 et qui vaut, pour notre exemple et pour ![]() ,
,
![]() d'où une fréquence
d'où une fréquence
![]() . En régime transitoire, on constate que l'on obtient une réponse oscillante faiblement amortie qui est dûe à un coefficient d'amortissement (
. En régime transitoire, on constate que l'on obtient une réponse oscillante faiblement amortie qui est dûe à un coefficient d'amortissement (![]() ) trop faible. En effet, d'après 5.1.2, on a
) trop faible. En effet, d'après 5.1.2, on a ![]() pour la même valeur de
pour la même valeur de ![]() . On diminue
. On diminue ![]() en augmentant
en augmentant ![]() (pour
(pour ![]() ,
, ![]() ) mais on augmente également
) mais on augmente également ![]() (pour
(pour ![]() ,
, ![]() ). Le problème, d'une manière plus générale, est que ce système, en boucle ouverte, possède une marge de phase trop faible (
). Le problème, d'une manière plus générale, est que ce système, en boucle ouverte, possède une marge de phase trop faible (
![]() ) comme indiqué sur le diagramme de Bode 5.5 à la pulsation de coupure
) comme indiqué sur le diagramme de Bode 5.5 à la pulsation de coupure ![]() . Ainsi, les conditions de performance du système asservi ne peuvent être assurées sans compromettre la stabilité de ce dernier. Une solution consiste à augmenter la marge de phase du système asservi en rajoutant un correcteur à avance de phase.
. Ainsi, les conditions de performance du système asservi ne peuvent être assurées sans compromettre la stabilité de ce dernier. Une solution consiste à augmenter la marge de phase du système asservi en rajoutant un correcteur à avance de phase.
guillaume 2008-11-17