suivant: Fonctionnement à vitesse variable monter: Régime transitoire précédent: Régime transitoire Table des matières
On considère que la vitesse de rotation est constante, égale à la valeur ![]() et que les variables subissent des petites variations autour d'un point de fonctionnement défini par l'indice 0.
Les relations matricielles entre les petites variations, en considérant la variation de vitesse négligeable, sont:
et que les variables subissent des petites variations autour d'un point de fonctionnement défini par l'indice 0.
Les relations matricielles entre les petites variations, en considérant la variation de vitesse négligeable, sont:
![\begin{displaymath}
\left[
\begin{array}{c}
-\sqrt{3}V_{s0}\cos{\delta_0}\Delta\...
...+
\left[\begin{array}{c}
0 K_e\omega_{m0}
\end{array}\right]
\end{displaymath}](img390.png) |
(1.100) |
On obtient alors entre les petites variations, des relations de transfert:
| (1.101) |
| (1.102) |
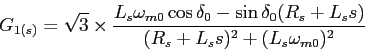 |
(1.103) |
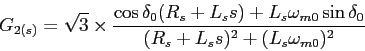 |
(1.104) |
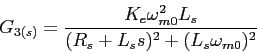 |
(1.105) |
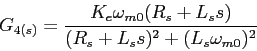 |
(1.106) |
Au vu de ses fonctions de transfert, on peut vérifier que la stabilité est assurée pour tout point de fonctionnement. Les pôles des fonctions sont:
Pour les variations de la tension statorique ou de l'angle ![]() , les pôles dominants sont
, les pôles dominants sont ![]() et
et ![]() dont la partie réelle est constante et la partie imaginaire variable avec la vitesse. Ainsi, plus la vitesse de la machine est élevée, plus les courants ont des réponses oscillatoires amorties dont l'amortissement diminue avec l'augmentation de la vitesse. Si l'on considère maintenant les numérateurs des fonctions de transfert et que
dont la partie réelle est constante et la partie imaginaire variable avec la vitesse. Ainsi, plus la vitesse de la machine est élevée, plus les courants ont des réponses oscillatoires amorties dont l'amortissement diminue avec l'augmentation de la vitesse. Si l'on considère maintenant les numérateurs des fonctions de transfert et que
![]() .
.
Dans le fonctionnement en moteur (![]() ), on trouve que seule
), on trouve que seule ![]() peut avoir un zéro positif correspondant à une réponse non minimale de phase. C'est le cas si
peut avoir un zéro positif correspondant à une réponse non minimale de phase. C'est le cas si
Dans le fonctionnement en génératrice, (![]() ), seule
), seule ![]() peut avoir un zéro positif si:
peut avoir un zéro positif si:
Dans les fonctionnements de la machine synchrone à aimant permanent et autopilotée dans laquelle on suppose la vitesse constante durant les régimes transitoires électriques, la stabilité asymptotique est vérifiée pour tous les fonctionnements. Seules les réponses des courants aux variations de l'angle ![]() peuvent être non minimales de phase. B.de Fornel montre que l'analyse effectuée par la méthode des petites variations donne des résultats qui s'avèrent identiques pour des variations d'amplitude finie. On peut ainsi avoir des informations précieuses sur le comportement transitoire des variables électriques de la machine synchrone.
peuvent être non minimales de phase. B.de Fornel montre que l'analyse effectuée par la méthode des petites variations donne des résultats qui s'avèrent identiques pour des variations d'amplitude finie. On peut ainsi avoir des informations précieuses sur le comportement transitoire des variables électriques de la machine synchrone.
guillaume 2008-11-17