Les équations de la machine synchrone à aimant permanent sont données par:
 |
(1.95) |
 |
(1.96) |
Le système d'équations différentielles ainsi obtenu présente une non linéarité du fait des produits
 et sa résolution doit s'effectuer par une méthode numérique ou analogique. L'interprétation physique des phénomènes transitoires est cependant plus aisée lorsque l'on peut recourir à une résolution analytique. Celle-ci n'est possible que si le système est linéaire, c'est à dire lorsque la vitesse
et sa résolution doit s'effectuer par une méthode numérique ou analogique. L'interprétation physique des phénomènes transitoires est cependant plus aisée lorsque l'on peut recourir à une résolution analytique. Celle-ci n'est possible que si le système est linéaire, c'est à dire lorsque la vitesse  peut être considérée comme constante ou lorsque le système peut être linéarisé dans le cas d'une variation de faible amplitude d'une grandeur électrique ou mécanique [62] [63]. Une étude menée par B. de Fornel dans [23] sur la stabilité et la recherche des modes dominants permet de conclure sur ces conditions en régime transitoire. Dans un système d'axes lié au champ tournant et tel que l'axe direct est suivant l'inducteur, les relations, sous forme matricielle et pour une machine à pôles lisses, deviennent:
peut être considérée comme constante ou lorsque le système peut être linéarisé dans le cas d'une variation de faible amplitude d'une grandeur électrique ou mécanique [62] [63]. Une étude menée par B. de Fornel dans [23] sur la stabilité et la recherche des modes dominants permet de conclure sur ces conditions en régime transitoire. Dans un système d'axes lié au champ tournant et tel que l'axe direct est suivant l'inducteur, les relations, sous forme matricielle et pour une machine à pôles lisses, deviennent:
![\begin{displaymath}
\left[
\begin{array}{c}
-\sqrt{3}V_s\sin{\delta}\\
\sqrt{3}...
...ht]+
\left[\begin{array}{c}
0 K_e\omega_m
\end{array}\right]
\end{displaymath}](img386.png) |
(1.97) |
avec l'équation mécanique
 |
(1.98) |
et
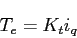 |
(1.99) |
Sous-sections
guillaume
2008-11-17

![\begin{displaymath}
\left[
\begin{array}{c}
-\sqrt{3}V_s\sin{\delta}\\
\sqrt{3}...
...ht]+
\left[\begin{array}{c}
0 K_e\omega_m
\end{array}\right]
\end{displaymath}](img386.png)