Modulation vectorielle

Cette modulation est utilisée dans les commandes modernes des machines pour obtenir des formes d'onde arbitraires non nécessairement sinusoïdales. Les tensions de référence sont les tensions simples désirées $V_{ni}$. Cette technique suit les principes suivants:

• le signal de référence est échantillonné à intervalles réguliers T (M.L.I régulière),
• pour chaque phase, réalisation d'une impulsion de largeur T centrée sur la période (M.L.I symétrique) dont la valeur moyenne est égale à la valeur de référence à l'instant d'échantillonnage.
• tous les interrupteurs d'un même demi-pont ont un état identique au centre et aux deux extrémités de la période.

Cette modulation est conduite en synchronisme sur les trois phases. Elle est appelée M.L.I vectorielle.

Considérons un onduleur triphasé dont les trois phases, notées A, B et C, sont reliées par une charge équilibrée en étoile à un neutre noté N. O est le point milieu de l'alimentation continue de cet onduleur au potentiel $+\frac{E}{2}$.

Les tensions composées ou entre phases s'écrivent alors:

$$U_{AB}=V_{A0}-V_{B0}$$

$$U_{BC}=V_{B0}-V_{C0}$$

$$U_{CA}=V_{C0}-V_{A0}$$

Les tensions simples, qui sont les tensions entre phases et neutre, sont liées aux tensions composées par:

$$U_{AB}=V_{AN}-V_{BN}$$

$$U_{BC}=V_{BN}-V_{CN}$$

$$U_{CA}=V_{CN}-V_{AN}$$

Lorsque le système est équilibré, on a:

$$V_{AN}=V_{BN}=V_{CN}=0$$

En combinant les relations précédentes pour obtenir les stensions simples, on a:

$$V_{AN}=\frac{1}{3}(U_{AB}-U_{CA})$$

$$V_{BN}=\frac{1}{3}(U_{BC}-U_{AB})$$

$$V_{CN}=\frac{1}{3}(U_{CA}-U_{BC})$$

Alors, en remplaçant par les relations des tensions composées, on obtient:

$$V_{AN}=\frac{1}{3}(2V_{A0}-V_{B0}-V_{C0})$$

$$V_{BN}=\frac{1}{3}(2V_{B0}-V_{C0}-V_{A0})$$

$$V_{CN}=\frac{1}{3}(2V_{C0}-V_{A0}-V_{B0})$$

Le potentiel du point neutre au point milieu fictif 0 est donné par:

$$V_{N0}=-V_{AN}+V_{A0}$$

d'où

$$V_{N0}=\frac{1}{3}(V_{A0}+V_{B0}+V_{C0})$$

Pour simplifier les calculs et représenter ces tensions, nous appliquons la transformation triphasée/diphasé de Concordia décrite en annexe D dans la section D.3. Seules les tensions simples y sont traitées mais l'on prouve que, pour un système triphasé équilibré, la transformation des tensions composées amène aux mêmes résultats. Ce qui évite ainsi de soustraire la tension $V_{N0}$ aux tensions de sortie de l'onduleur. Ceci permet alors d'alléger un peu le modèle de l'onduleur. Une analyse combinatoire de tous les états possibles des interrupteurs permet de calculer les vecteurs de tension $V_{\alpha}$ et $V_{\beta}$. On obtient ainsi le tableau 1.1.

Tableau 1.1: Combinaisons des interrupteurs et valeurs des vecteurs tension associées

$T_1$	$T_2$	$T_3$	$V_{A0}$	$V_{B0}$	$V_{C0}$	$V_{AN}$	$V_{BN}$	$V_{CN}$	$V_{\alpha}$	$V_{\beta}$
0	0	0	$-\frac{E}{2}$	$-\frac{E}{2}$	$-\frac{E}{2}$	0	0	0	0	0	$\vec V_0$
0	0	1	$-\frac{E}{2}$	$-\frac{E}{2}$	$\frac{E}{2}$	$-\frac{E}{3}$	$-\frac{E}{3}$	$-\frac{E}{3}$	$-\frac{E}{\sqrt{6}}$	$-\frac{E}{\sqrt{2}}$	$\vec V_5$
0	1	0	$-\frac{E}{2}$	$\frac{E}{2}$	$-\frac{E}{2}$	$-\frac{E}{3}$	$\frac{2E}{3}$	$-\frac{E}{3}$	$-\frac{E}{\sqrt{6}}$	$\frac{E}{\sqrt{2}}$	$\vec V_3$
0	1	1	$-\frac{E}{2}$	$\frac{E}{2}$	$\frac{E}{2}$	$-\frac{2E}{3}$	$\frac{E}{3}$	$\frac{E}{3}$	$-\frac{\sqrt{2}E}{\sqrt{6}}$	$0$	$\vec V_4$
1	0	0	$\frac{E}{2}$	$-\frac{E}{2}$	$-\frac{E}{2}$	$\frac{2E}{3}$	$-\frac{E}{3}$	$-\frac{E}{3}$	$\frac{\sqrt{2}E}{\sqrt{3}}$	$0$	$\vec V_1$
1	0	1	$\frac{E}{2}$	$-\frac{E}{2}$	$\frac{E}{2}$	$\frac{E}{3}$	$-\frac{2E}{3}$	$\frac{E}{3}$	$\frac{E}{\sqrt{6}}$	$-\frac{E}{\sqrt{2}}$	$\vec V_6$
1	1	0	$\frac{E}{2}$	$\frac{E}{2}$	$-\frac{E}{2}$	$\frac{E}{3}$	$\frac{E}{3}$	$-\frac{2E}{3}$	$\frac{E}{\sqrt{6}}$	$\frac{E}{\sqrt{2}}$	$\vec V_2$
1	1	1	$\frac{E}{2}$	$\frac{E}{2}$	$\frac{E}{2}$	0	0	0	0	0	$\vec V_7$

On peut alors représenter les vecteurs définis précédemment dans un polygone (figure 1.24) dit polygone de commutation en fonction des valeurs que prennent $V_{\alpha}$ et $V_{\beta}$.

Figure 1.24: Polygone de commutation.

Il s'agit de déterminer la position du vecteur de consigne dans ce repère et le secteur dans lequel il se situe. Celui-ci est limité par deux des vecteurs définis dans le tableau 1.1 et si on lui affecte un angle $\gamma$, comme représenté sur la figure 1.25, on reconstitue les tensions de référence part moyenne de ces vecteurs. Ainsi, on définit $V_{s\alpha}=V_s\sin{(\pi/3 -\gamma)}$ et $V_{s\beta}=V_s\sin{(\gamma)}$ en fonction des temps d'application des séquences définies précédemment avec $T_1$ qui est le temps d'application de $\vec V_1$, $T_2$ celui de $\vec V_2$ et ainsi de suite.

Figure 1.25: Exemple de calcul de $T_1$ et $T_2$.

On a donc, dans le secteur I, les égalités suivantes:

$$V_s\sin{(\gamma)}=V_2\frac{T_2}{T}\cos{(\pi/6)}=V_2\frac{T_2}{T}\frac{\sqrt{3}}{2}$$

d'où

$$V_s\sin{(\gamma)}=V_{S\beta}=\frac{E}{\sqrt{2}}\frac{T_2}{T}$$

alors

$$T_2=\frac{\sqrt{2}V_{s\beta}}{E}T$$

et

$$V_s\sin{(\pi/3-\gamma)}=\cos{(\pi/6)}V_1\frac{T_1}{T}$$

d'où

$$T1=\frac{\sqrt{2}}{E}V_s\sin{(\pi/3-\gamma)}T=\frac{\sqrt{2}}... ...(\frac{\sqrt{3}}{2}\cos{\gamma}-\frac{1}{2}\sin{\gamma}\right)T$$

alors

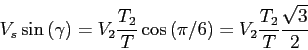
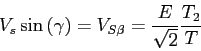
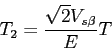
$$T_1=\frac{\sqrt{6}V_{s\alpha}-\sqrt{2}V_{s\beta}}{2E}T$$

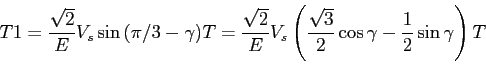
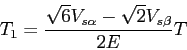
Comme l'on veut que la M.L.I soit symétrique et centré sur la période T, on utilise les vecteurs $\vec V_0$ et $\vec V_7$ en les répartissant 2 au centre et 2 à l'extérieur dans cette période pendant une durée $T_i$ valant $T_i=\frac{T-T_1-T_2}{4}$ [18]. On obtient alors la séquence de la figure 1.26.

Figure 1.26: Séquence des vecteurs.

On effectue les mêmes calculs pour les autres secteurs, on obtient alors:

secteur II:

$$T_2=\frac{\sqrt{6}V_{s\alpha}-\sqrt{2}V_{s\beta}}{2E}T$$

$$T_3=\frac{-\sqrt{6}V_{s\alpha}+\sqrt{2}V_{s\beta}}{2E}T$$

$$T_i=\frac{T-T_2-T_3}{4}$$

secteur III:

$$T_3=\frac{\sqrt{2}V_{s\beta}}{E}T$$

$$T_4=\frac{-\sqrt{6}V_{s\alpha}-\sqrt{2}V_{s\beta}}{2E}T$$

$$T_i=\frac{T-T_3-T_4}{4}$$

secteur IV:

$$T_4=\frac{-\sqrt{6}V_{s\alpha}+\sqrt{2}V_{s\beta}}{2E}T$$

$$T_5=\frac{-\sqrt{2}V_{s\beta}}{E}T$$

$$T_i=\frac{T-T_4-T_5}{4}$$

secteur V:

$$T_5=\frac{-\sqrt{6}V_{s\alpha}-\sqrt{2}V_{s\beta}}{2E}T$$

$$T_6=\frac{\sqrt{6}V_{s\alpha}-\sqrt{2}V_{s\beta}}{2E}T$$

$$T_i=\frac{T-T_5-T_6}{4}$$

secteur VI:

$$T_6=\frac{-\sqrt{2}V_{s\beta}}{E}T$$

$$T_1=\frac{\sqrt{6}V_{s\alpha}+\sqrt{2}V_{s\beta}}{2E}T$$

$$T_i=\frac{T-T_6-T_1}{4}$$

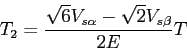
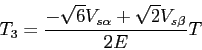
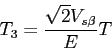
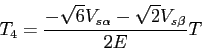
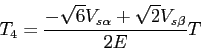
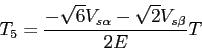
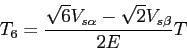
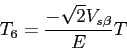
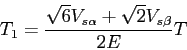
Le choix de la séquence se réalise en testant les tensions $V_{s\alpha}$ et $V_{s\beta}$. On obtient ainsi un algorithme qui, suivant les résultats des tests, appelle les calculs des temps du secteur correspondant cités précédemment [33].

Etant donné que l'on a un temps minimal de conduction $t_{min}$ équivalent à l'impulsion minimale requise de $2T_i$, alors, on peut exprimer la tension simple maximale comme étant, par définition pour un circuit en étoile, le rapport entre la tension entre ligne et $\sqrt{3}$ pondéré par un hachage minimum dû au temps $t_{min}$ soit:

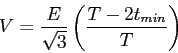$$V=\frac{E}{\sqrt{3}}\left(\frac{T-2t_{min}}{T}\right)$$ (1.93)

L'influence du temps mort $t_m$, qui est le temps entre une extinction immédiate et l'amorçage, vient également s'ajouter à cette pondération, d'où:

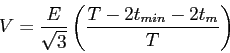$$V=\frac{E}{\sqrt{3}}\left(\frac{T-2t_{min}-2t_m}{T}\right)$$ (1.94)

Ce type de modulation est également appelé modulation postcalculée car on effectue le calcul des angles de commutation en ligne.