suivant: Inductance mutuelles relatives à monter: Modélisation du moteur synchrone précédent: Inductance propre rotorique Table des matières
Dans une machine à pôles lisses, abstraction faite de la faible variation de perméance du circuit magnétique rotorique selon les axes d et q due à l'absence d'encoches dans la zone centrale des pôles, le circuit magnétique est pratiquement isotrope. On peut donc modéliser les inductances propres statoriques par de simples inductances notées ![]() ,
, ![]() et
et ![]() sachant que:
sachant que:
![]()
Les termes ![]() et
et ![]() désignent respectivement l'inductance principale et l'inductance de fuite.
désignent respectivement l'inductance principale et l'inductance de fuite.
Les inductances de fuite correspondent aux flux couplés uniquement avec l'enroulement qui les crée. Les lignes de champ traversant l'entrefer et couplées avec l'enroulement du stator appartiennent au flux commun tandis que les lignes se fermant autour des encoches et des connexions frontales constituent des flux de fuite couplés avec l'enroulement rotorique seulement. On distingue usuellement:
Dans une machine à pôles saillants, la perméance du circuit magnétique est différente selon l'axe d et l'axe q. Soient ![]() et
et ![]() les valeurs extrêmes de la perméance. En pratique, les règles adoptées pour le dimensionnement des épanouissements polaires et la forme de l'entrefer conduisent à une variation pratiquement sinusoïdale de
les valeurs extrêmes de la perméance. En pratique, les règles adoptées pour le dimensionnement des épanouissements polaires et la forme de l'entrefer conduisent à une variation pratiquement sinusoïdale de
![]() entre ces deux extrêmes.
Si
entre ces deux extrêmes.
Si ![]() désigne la solénation pulsante de la phase (a), ses projections sur les axes d et q valent:
désigne la solénation pulsante de la phase (a), ses projections sur les axes d et q valent:
Les flux correspondants créées par ces composantes sont:
Les flux totalisés couplés avec la phase a s'obtiennent en multipliant par ![]() les flux précédents 1.5 et 1.6:
les flux précédents 1.5 et 1.6:
| (1.7) |
| (1.8) |
où ![]() représente le nombre de spires en série et
représente le nombre de spires en série et ![]() le facteur d'enroulement à intégrer à l'expression du fondamental de la tension induite.
le facteur d'enroulement à intégrer à l'expression du fondamental de la tension induite.
Le facteur d'enroulement est le produit du facteur de distribution ![]() par le facteur de raccourcissement du pas
par le facteur de raccourcissement du pas ![]() associé au fondamental. Soit, pour un nombre d'encoches par pôle et par phase
associé au fondamental. Soit, pour un nombre d'encoches par pôle et par phase ![]() et pour un nombre de pôles (n), nous avons:
et pour un nombre de pôles (n), nous avons:
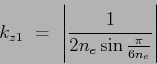 |
(1.9) |
et
| (1.10) |
donc
| (1.11) |
Exemple:
Pour ![]() et
et
![]() alors:
alors:
On trouve également un facteur d'enroulement ![]() pour les harmoniques de rang
pour les harmoniques de rang ![]() qui est toujours le produit vu précédemment mais associé aux harmoniques. Les facteurs de distribution et d'enroulement correspondant sont alors donnés par:
qui est toujours le produit vu précédemment mais associé aux harmoniques. Les facteurs de distribution et d'enroulement correspondant sont alors donnés par:
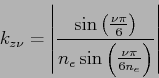 |
(1.12) |
et
| (1.13) |
ainsi que
| (1.14) |
Pour l'exemple précédent, nous avons:
On constate alors que la distribution de l'enroulement assure une réduction substantielle des harmoniques de tension et que le raccourcissement du pas proposé permet d'éliminer presque complètement la tension harmonique de rang ![]() .
.
Le flux totalisé résultant couplé avec la phase a s'obtient en projetant ![]() et
et ![]() sur l'axe de la phase a:
sur l'axe de la phase a:
| (1.15) |
En posant:
L'inductance principale ![]() s'exprime comme:
s'exprime comme:
| (1.18) |
d'où
| (1.19) |
avec
L'inductance propre d'une phase inclut l'inductance de fuite de sorte que:
| (1.22) |
Les inductances
![]() et
et
![]() s'obtiennent de la relation précédente en remplaçant
s'obtiennent de la relation précédente en remplaçant ![]() respectivement par
respectivement par
![]() et
et
![]() :
:
| (1.23) |
| (1.24) |
guillaume 2008-11-17