suivant: Loi d'Ampère monter: Aimants permanents précédent: Rappel sur les circuits Table des matières
| (C.3) |
Elles sont complétées par des relations spécifiques aux matériaux:
| (C.7) |
Si A est un vecteur défini selon trois axes x,y et z par


alors, par définition, on a:
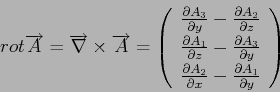 |
(C.8) |
 |
(C.9) |
Dans l'étude des phénomènes associés à la conversion électromécanique, les fréquences en jeu sont relativement faibles, ne dépassant guère quelques dizaines de KHz. Dans ces conditions, la dérivée du vecteur déplacement de l'équation C.1 peut être négligée vis-à-vis de la densité de courant J. On obtient alors :
De plus, les équations C.4 et C.6 ne présente plus d'intérêt. On parlera de régime quasi statique des équations de Maxwell. Ces relations vectorielles utilisées dans l'étude de certains phénomènes particuliers (pertes par courants de Foucault, effet pelliculaire) se prêtent mal à l'étude du comportement des machines en régime transitoire ou permanent. Bien que d'intéressantes solutions à ce problème, faisant appel au vecteur de Poynting, aient été développées [37], on préfère utiliser les formes intégrales des lois de Maxwell et recourir au modèle de Kirchhoff caractérisé par la notion de circuit et les équations associées.
guillaume 2008-11-17